跑酷文明
题目描述:
小 A 有 \( n \) 个无限大的网格图,每张图上都分布着密度各异的格点。
对于第 \( i \) 张网格图(\( 1 \le i \le n \)),其上相邻格点间的距离为 \( i + 1 \)。更具体地:
- 网格图 \( i \) 上的坐标 \( (x, y) \) 有格点,当且仅当存在整数 \( a, b \) 满足 \( x = (i + 1) \times a \),\( y = (i + 1) \times b \)。
小 A 将这 \( n \) 张网格图对齐叠加,形成了一张新的复合网格图。在复合网格图上,一个位置处有格点,当且仅当该位置在至少一张网格图上有格点(如果多张网格图的同一位置都有格点,它们会在复合网格图上合并为一个)。
接下来,小 A 选定复合网格图上的一个矩形区域,矩形区域的左下角坐标为 \( (x_1, y_1) \),右上角坐标为 \( (x_2, y_2) \)。
你的任务是,求出该矩形区域内(包含边界)的格点数量。
输入格式:
输入格式如下:
\( \quad \begin{matrix} n \\ x_1 & y_1 \\ x_2 & y_2 \end{matrix} \)
输出格式:
输出一行一个整数,代表区域内可见的格点数。
样例输入:
样例1 2 -1 -1 1 1 样例2 3 1 1 6 10
样例输出:
样例1 1 样例2 20
提示:
样例解释 #1
唯一的格点在 \( (0, 0) \) 处。
样例解释 #2
该区域的格点分布如下:
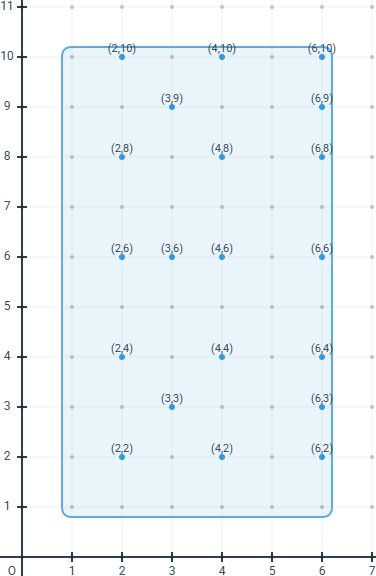
对于所有数据:
- \( 1 \le n \le 10^7 \)
- \( -10^7 \le x_1 \le x_2 \le 10^7 \)
- \( -10^7 \le y_1 \le y_2 \le 10^7 \)
| 子任务 | 分值 | 附加约束 |
| \( \bf1 \) | \( 17 \) | \( n \le 3 \);\( |x_i|, |y_i| \le 100 \) |
| \( \bf2 \) | \( 14 \) | \( n \le 10^3 \);\( |x_i|, |y_i| \le 10^3 \) |
| \( \bf3 \) | \( 16 \) | \( n \le 10^3 \) |
| \( \bf4 \) | \( 18 \) | \( n \le 10^6 \) |
| \( \bf5 \) | \( 15 \) | \( |x_i|, |y_i| \le 10^6 \) |
| \( \bf6 \) | \( 11 \) | \( x_1, y_1 = 1 \);\( x_2, y_2 = n \) |
| \( \bf7 \) | \( 9 \) | \( - \) |
时间限制: 2000ms
空间限制: 512MB
来源: KonataAFO