直方图的水量

题目描述:

给定一个直方图(也称柱状图)，假设有人从上面源源不断地倒水，最后直方图能存多少水量?直方图的宽度为 1。

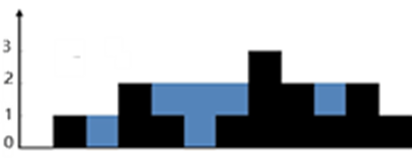
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图，在这种情况下，可以接 6 个单位的水（蓝色部分表示水）。

输入格式:

输入一排直方图的高度，以逗号分隔。

输出格式:

一个整数，表示总的水量。

数据范围:

60%的数据，\( 3 \le n \lt 10,000 \)

100%的数据，\( 3 \le n \le 100,000 \)

每个直方图的高度在1000以内。

样例输入:

[0,1,0,2,1,0,1,3,2,1,2,1]

样例输出:

6

提示:

算法一：前缀思想

请完善程序：

#L[]前缀最大值， R[]是后缀最大值
s = input()
s = s[ 1:len(s)-1 ]
a = list( map( int , ______________ ) )
a = [0] + a
n = len( a ) - 1
L = [ 0 for i in range( n + 1 ) ]
R = [ 0 for i in range( n + 1 ) ]
L[1] = a[1]
for i in range( 2, n+1):  L[i] = ________________
R[n] = a[n]
for i in range( n-1, 0, -1 ): R[i] = ________________
ans = 0
for i in range( 1, n+1 ):
    ans += ______________________
print( ans )

算法二：单调栈

每个元素进栈前，把栈项小于等于它的元素弹掉，被弹掉的元素就可以结算了

结算对答案的贡献为：当前元素或新栈项元素的较小高度值 *  当前元素和新栈顶元素之间的宽度。

 

算法三：双指针

每列都及时考虑掉，每列对答案的积水贡献量为：min(（ 左边最大值，右边最大值 ） - heght[ i ]。

维护好，左边的最大值 和 右边的最大值。

时间限制: 1000ms
空间限制: 256MB

---