一列货运列车有 n 节车厢，每节车厢将停放在不同车站。假定 n 个车站的编号分别为1 ~ n，列车按照第 n 站至第 1 站的顺序停靠，车厢编号与目的站序号相同。为了到每个站时只需卸掉最后一节车厢，必须将任意次序的车厢进行重排，使得各车厢从前往后的编号是 1 ~ n。重排车厢的工作在一个转轨站里完成，如图所示，在转轨站中有一个入轨，一个出轨和 k（k=3）个缓冲轨H1, H2, H3。开始时 n 节车厢从入轨处进入转轨站，转轨结束后车厢按编号1~n的次序离开转轨站。

编写程序模拟有n（ n=9 ）节车厢的“入轨”和“出轨”过程,（入轨车厢次序满足缓冲轨为3的情况）。车厢可以从入轨的前部移动到一个缓冲轨的顶部或者是出轨处的后部。进入缓冲轨的车厢编号要满足：

① 小于要进入的缓冲轨的栈顶元素编号。

② 满足条件①里面栈顶元素编号最小的缓冲轨。

③ 若没有满足条件 ① 的缓冲轨，则进入空的缓冲轨。

共两行。

第一行是n列车的排列序号，以空格隔开。

第二行一个整数k，表示有个k个缓冲轨。

见样例输出。

n <= 10

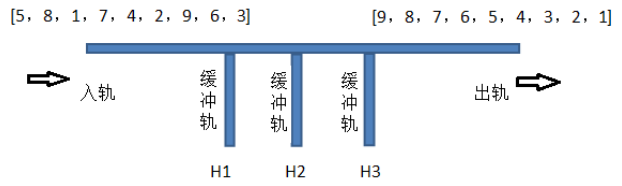
请完善程序：

def inputStack(bh,stacks,n): # 将车厢移到缓冲轨处 
    global k 
    bestStack = -1 # bestStack 记录最小车厢编号所在的缓冲轨编号 
    bestTop = n + 1 # bestTop 记录缓冲轨中的最小车厢编号 
    for i in range(k): 
        if len(stacks[i])>0: 
            top = stacks[i][-1] 
            if ________________________ :    #填空1
                bestTop = top 
                bestStack = i 
        else: 
            if bestStack == -1: 
                bestStack = i 
    if bestStack == -1:
        return False
    stacks[bestStack].append(bh)
    print('Move carriage %d from the track entry point to the buffer track H%d.' % ( bh, bestStack+1 ) )

def output( stacks, n ):
    # 将缓冲轨中的剩余车厢按顺序依次移到出轨处
    while True:
        minNum = n + 1 
        for j in range(k):
            if len(hStacks[j]) > 0:
                if hStacks[j][-1] < minNum:
                    minNum = hStacks[j][-1]
                    minStack=j
        if minNum == n + 1:
            break
        print("Move carriage %d from buffer track H%d to the derailment point." % ( minNum, minStack+1 ) )
        hStacks[minStack].pop()

# 主程序开始
list1 = list( map( int, input().split(' ') ) )
n = len( list1 )
k = int( input() )
hStacks = [ __________ for i in range(k) ]    #填空2
curBH = 1
minStack = -1 
print("The process of car rearrangement is as follows:")
i = 0
while i < n:
    if list1[i] == curBH:
        print("Move carriage %d directly from the track entry point to the derailment point." % list1[i])
        ______________________   #填空3
        i += 1
        _____________________    #填空4
    while True:
        minNum = n + 1 
        for j in range(k):
            if len( hStacks[j] ) > 0:
                if hStacks[j][-1] < minNum:
                    minNum = hStacks[j][-1]
                    minStack=j
        if minNum == curBH:
            print( "Move carriage %d from buffer track H%d to the derailment point." % ( minNum, minStack+1 ) )
            hStacks[ minStack ].pop()
            _______________________      #填空5
        else:
            ___________________________      #填空6
            i += 1;    break
while curBH < n+1:
    output( hStacks, n ); curBH += 1
print( "Complete carriage rearrangement!" )