求正方形面积

题目描述:

某个棋盘有rows行cols列。棋盘上的每个格子都上有黑色或白色棋子。现在想要找出黑棋区域最大的正方形面积。例如某棋盘的状态如图所示。

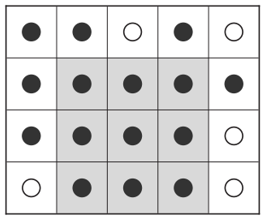
在该棋盘中黑棋区域最大的正方形为3×3(阴影区域) ， 即最大面积为9。小明编写程序求解该问题。用二维数组matrix表示棋盘， 在数组中用1表示黑色棋子，用0表示白色棋子。

输入格式:

第一行两个数表示行rows与列cols

第二行开始给定一个rows * cols的01矩阵，两个数之间用一个空格隔开

输出格式:

一个整数表示最大的正方形面积。

样例输入:

8 10
0 1 1 0 0 0 1 1 0 0
1 1 0 1 0 1 1 0 0 0 
0 1 1 1 0 1 1 1 1 0
0 1 1 1 1 1 0 0 1 0
1 1 1 1 1 1 0 0 1 1
1 0 1 1 0 1 1 1 1 0
0 1 0 0 1 1 1 0 1 0
0 1 1 0 1 1 1 1 1 1

样例输出:

9

提示:

rows, cols = map( int , input().split() )
matrix=[ ]
for i in range(rows):
    s = list( map( int , input().strip().split() ) )
    matrix.append(  s )
'''
print("======棋盘状态========")
for x in matrix:
    print(x)
print("=====================")
'''
max_side = 0
dp = ______①______
#dp存储以matrix[i][j]可为右下角元素的最大正方形的边长
for i in range(rows):
    for j in range( cols ):
        #当前的值为1时，求构成正方形的最长边
        if matrix[i][j] == 1:
            #当前值为1，处于首行首列时
            if ______②_____ :
                dp[i][j] = 1
            else:
                dp[i][j] = ____________③______________
            if dp[i][j] > max_side:
                max_side=dp[i][j]
square = ________④_________
print( square )

时间限制: 1000ms
空间限制: 256MB

---